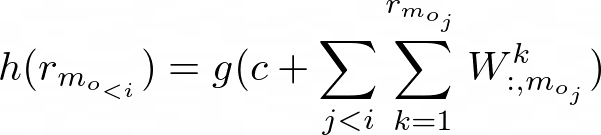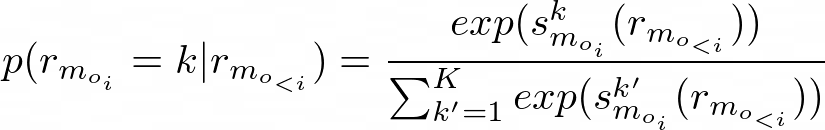One of the best AI-related books that I read last year is Terrence Sejnowski’s “The Deep Learning Revolution.” The book explains how deep learning went from being an obscure academic field to an impactful technology in the information era. The author, Terry Sejnowski is one of the pioneers of deep learning who, together with Geoffrey Hinton, created Boltzmann machines: a deep learning network that has remarkable similarities to learning in the brain.

The Deep Learning Revolution (https://mitpress.mit.edu/books/deep-learning-revolution)

I recently listened to a podcast on Eye on AI where Terrence discussed machines dreaming, the birth of the Boltzmann machines, the inner-workings of the brain, and the process to recreate them in neural networks. In particular, he and Geoff Hinton invented the Boltzmann machine with a physics-inspired architecture:

Each unit has a probability to have an output that varies with the amount of input that is being given.
They gave the network input and then kept track of the activity patterns within the network. For each connection, they kept track of the correlation between the input and the output. Then in order to be able to learn, they got rid of the inputs and let the network run free, which is called the sleep phase.
The learning algorithm is intuitive: They subtracted the sleep phase correlation from the wake learning phase and then adjusted the weights accordingly. With a big enough dataset, this algorithm can effectively learn arbitrary mappings between input and output.

The Boltzmann machine analogy turns out to be a good insight into what’s happing in the human brain during sleep. In cognitive science, there’s a concept called replay, where the hippocampus plays back our memories and experiences to the cortex, and then the cortex integrates that into the semantic knowledge base that we have about the world.

That’s a long-winded way to say that I have been interested in exploring Boltzmann machines for a while. And I was quite ecstatic to see their applications in the context of recommendation systems!

In this post and those to follow, I will be walking through the creation and training of recommendation systems, as I am currently working on this topic for my Master Thesis.

Part 1 provided a high-level overview of recommendation systems, how they are built, and how they can be used to improve businesses across industries.
Part 2 provided a helpful review of the ongoing research initiatives concerning the strengths and application scenarios of these models.
Part 3 provided a couple of research directions that might be relevant to the recommendation system scholar community.
Part 4 provided the nitty-gritty mathematical details of 7 variants of matrix factorization that can be constructed: ranging from the use of clever side features to the application of Bayesian methods.
Part 5 provided the architecture design of 5 variants of multi-layer perceptron based collaborative filtering models, which are discriminative models that can interpret the features in a non-linear fashion.
Part 6 provided a master class on six variants of autoencoders based collaborative filtering models, which are generative models that are superior in learning underlying feature representation.

In Part 7, I explore the use of Boltzmann Machines for collaborative filtering. More specifically, I will dissect three principled papers that incorporate Boltzmann Machines into their recommendation architecture. But first, let’s walk through a primer on Boltzmann Machine and its variants.

A Primer on Boltzmann Machine and Its Variants

According to its inventor:

“A Boltzmann Machine is a network of symmetrically connected, neuron-like units that make stochastic decisions about whether to be on or off. Boltzmann machines have a simple learning algorithm that allows them to discover interesting features in datasets composed of binary vectors. The learning algorithm is very slow in networks with many layers of feature detectors, but it can be made much faster by learning one layer of feature detectors at a time.”

To unpack this further, Hinton states that we can use Boltzmann machines to tackle two different sets of computational problems:

Search Problem: Boltzmann machines have fixed weights on the connections, which are used as the cost function of an optimization procedure.
Learning Problem: Given a set of binary data vectors, our goal is to find the weights on the connections to optimize the training process. Boltzmann machines update the weights’ values by solving many iterations of the search problem.

A Restricted Boltzmann Machine (RBM) is a specific type of a Boltzmann machine, which has two layers of units. As illustrated below, the first layer consists of visible units, and the second layer includes hidden units. In this restricted architecture, there are no connections between units in a layer.

Manish Nayak — An Intuitive Introduction of RBM (https://medium.com/datadriveninvestor/an-intuitive-introduction-of-restricted-boltzmann-machine-rbm-14f4382a0dbb)

The visible units in the model correspond to the observed components, and the hidden units represent the dependencies between these observed components. The goal is to model a joint probability of visible and hidden units: p(v, h). Because there are no connections between hidden units, the learning is effective as all hidden units are conditionally independent, given the visible units.

A Deep Belief Network (DBN) is a multi-layer learning architecture that uses a stack of RBMs to extract a deep hierarchical representation of the training data. In such a design, the hidden layer of each sub-network serves as the visible layer for the upcoming sub-network.

Himanshu Singh — Deep Belief Networks: An Introduction (https://medium.com/analytics-army/deep-belief-networks-an-introduction-1d52bb867a25)

When learning through a DBN, firstly, the RBM in the bottom layer is trained by inputting the original data into the visible units. Then, the parameters are fixed up, and the hidden units of the RBM are used as the input into the RBM in the second layer. The learning process continues until reaching the top of the stacked sub-networks, and finally, a suitable model is obtained to extract features from the input. Since the learning process is unsupervised, it is common to add a new network of supervised learning to the end of the DBN to use it in a supervised learning task such as classification or regression (Logistic Regression layer in the image above).

Okay, it’s time to review the different Boltzmann Machines based recommendation framework!

1 — Restricted Boltzmann Machines for Collaborative Filtering

Recall in the classic collaborative filtering setting, we attempt to model the ratings (user-item interaction) matrix X with the dimension n x d, where n is the number of users, and d is the number of items. An entry xᵢⱼ (row i, column j) corresponds to user i’s rating for item j. In the MovieLens dataset (which has been used in all of my previous posts), xᵢⱼ ∈ 0, 1, 2, 3, 4, 5 (where 0 represents missing rating).

For example, xᵢⱼ = 2 means that user i has given movie j the rating 2 out of 5. On the other hand, xᵢⱼ = 0 means that the user has not rated the movie j.
The rows of X encode each user’s preference over all movies, and the columns of X encode each item’s ratings received by all users.

Formally speaking, we define prediction and inference in the collaborative filtering context as follows:

Prediction: Given the observed rating X, predict x_{im} (a rating that a user i has given for a new query movie m).
Inference: Compute the probability p(x_{im} = k | Xₒ) (where Xₒ denotes the non-zero entries of X and k ∈ 0, 1, 2, 3, 4, 5).

The RBM architecture proposed in “Restricted Boltzmann Machines for Collaborative Filtering.”

Salakhutdinov, Mnih, and Hinton framed the task of computing p(x_{im} = k | Xₒ) as inference on an underlying RBM with trained parameters. The dataset is sub-divided into rating matrices, where a user’s ratings are one-hot encoded into a matrix V such that vⱼᵏ = 1 if the user rates movie j with rating k. The figure above illustrates the RBM graph:

V is a 5 x d matrix that corresponds to one-hot encoded integer ratings of the user.
h is a F x 1 vector of binary hidden variables, where F is the number of hidden variables.
W is a d x F x 5 tensor that encodes adjacency between ratings and hidden features. Its entry Wⱼcᵏ corresponds to the edge potential between rating k of the movie j and the hidden feature c.

The whole user-item interaction matrix is a collection of V(s), where each V corresponds to each user’s ratings. Because each user can have different missing values, each will have a unique RBM graph. In each RBM graph, the edges connect ratings and hidden features but do not appear between items of missing ratings. The paper treats W as a set of edge potentials that are tied across all such RBM graphs.

In the training phase, RBM characterizes the relationship between the ratings and hidden features using conditional probabilities p(vⱼᵏ = 1 | h) and p(hₐ = 1 | V):

After getting these probabilities, there are two extra steps to compute p(vₒᵏ = 1 | V):

Compute the distribution of each hidden feature in h based on observed ratings V and the edge potentials W (p(hₐ = 1 | V) for each a).
Compute p(vₒᵏ = 1 | V) based on the edge potentials W and the distribution of p(hₐ = 1 | V).

In the optimization phase, W is optimized by the marginal likelihood of V — p(V). The gradient ∇ Wᵢⱼᵏ is computed using contrastive divergence, which is an approximation of the gradient-based on Gibbs sampling:

The expectation <.>_T represents a distribution of samples from running the Gibbs sampler, initialized at the data, for T full steps. T is typically set to 1 at the beginning of learning and increased as the learning converges. When running the Gibbs sampler, the RBM reconstructs (as seen in equation 1) the distribution over the non-missing ratings. The approximate gradients of contrastive divergence can then be averaged over all n users.

The PyTorch code of the RBM model class is given below for illustration purpose:

class RBM:
    def __init__(self, n_vis, n_hid):
        """
        Initialize the parameters (weights and biases) we optimize during the training process
        :param n_vis: number of visible units
        :param n_hid: number of hidden units
        """

        # Weights used for the probability of the visible units given the hidden units
        self.W = torch.randn(n_hid, n_vis)  # torch.rand: random normal distribution mean = 0, variance = 1

        # Bias probability of the visible units is activated, given the value of the hidden units (p_v_given_h)
        self.v_bias = torch.randn(1, n_vis)  # fake dimension for the batch = 1

        # Bias probability of the hidden units is activated, given the value of the visible units (p_h_given_v)
        self.h_bias = torch.randn(1, n_hid)  # fake dimension for the batch = 1

    def sample_h(self, x):
        """
        Sample the hidden units
        :param x: the dataset
        """

        # Probability h is activated given that the value v is sigmoid(Wx + a)
        # torch.mm make the product of 2 tensors
        # W.t() take the transpose because W is used for the p_v_given_h
        wx = torch.mm(x, self.W.t())

        # Expand the mini-batch
        activation = wx + self.h_bias.expand_as(wx)

        # Calculate the probability p_h_given_v
        p_h_given_v = torch.sigmoid(activation)

        # Construct a Bernoulli RBM to predict whether an user loves the movie or not (0 or 1)
        # This corresponds to whether the n_hid is activated or not activated
        return p_h_given_v, torch.bernoulli(p_h_given_v)

    def sample_v(self, y):
        """
        Sample the visible units
        :param y: the dataset
        """

        # Probability v is activated given that the value h is sigmoid(Wx + a)
        wy = torch.mm(y, self.W)

        # Expand the mini-batch
        activation = wy + self.v_bias.expand_as(wy)

        # Calculate the probability p_v_given_h
        p_v_given_h = torch.sigmoid(activation)

        # Construct a Bernoulli RBM to predict whether an user loves the movie or not (0 or 1)
        # This corresponds to whether the n_vis is activated or not activated
        return p_v_given_h, torch.bernoulli(p_v_given_h)

    def train(self, v0, vk, ph0, phk):
        """
        Perform contrastive divergence algorithm to optimize the weights that minimize the energy
        This maximizes the log-likelihood of the model
        """

        # Approximate the gradients with the CD algorithm
        self.W += (torch.mm(v0.t(), ph0) - torch.mm(vk.t(), phk)).t()

        # Add (difference, 0) for the tensor of 2 dimensions
        self.v_bias = torch.sum((v0 - vk), 0)
        self.h_bias = torch.sum((ph0 - phk), 0)

For my PyTorch implementation, I designed the RBM architecture with a hidden layer of 100 units activated by a non-linear sigmoid function. Other hyper-parameters include the batch size of 512 and epochs of 50.

2 — Explainable Restricted Boltzmann Machines for Collaborative Filtering

Explanations for recommendations can have multiple benefits, including effectiveness (helping users to make the right decisions), efficiency (assisting users to make faster decisions), and transparency (revealing the reasoning behind the recommendations). In the case of RBM, which assigns a low-dimensional set of features to items in a latent space, it is difficult to interpret these learned features. Therefore, a massive challenge is to choose an interpretable technique with moderate prediction accuracy for RBM.

Abdollahi and Nasraoui designed an RBM model for a collaborative filtering recommendation system that suggests items that are explainable while maintaining accuracy. The paper’s scope is limited to recommendations where no additional source of data is used in explanations, and where explanations for recommended items can be generated from the ratings given to these items, by the active user’s neighbors only.

An example of a user-based neighbor style explanation for a recommended item, as proposed in “Explainable RBM for CF.”

The main idea is that if many neighbors have rated the recommended item, then this could provide a basis upon which to explain the recommendations, using neighborhood-style explanation mechanisms. For user-based neighbor-style explanations, such as the one shown in the figure above, the Explainability Score of item i for user u is defined as:

Here N_k (u) is the set of user u’s k neighbors, r_{x, i} is the rating of x on item i, and R_max is the maximum rating value of N_k (u) on i. Cosine similarity defines the neighborhood. Without loss of information, r_{x, i} is 0 for missing ratings, indicating that user x does not contribute to the user-based neighbor-style explanation of item i for user u. Therefore, the Explainability Score is between 0 and 1. Item i is explainable for user u only if its explainability score is larger than 0. When no explanation can be made, the explainability ratio would be 0.

The TensorFlow code of the RBM model class is given below for illustration purpose:

def rbm(movies_df):
    """
    Implement RBM architecture in TensorFlow
    :param movies_df: data frame that stores movies information
    :return: variables to be used during TensorFlow training
    """
    hiddenUnits = 100  # Number of hidden layers
    visibleUnits = len(movies_df)  # Number of visible layers

    # Create respective placeholder variables for storing visible and hidden layer biases and weights
    vb = tf.placeholder("float", [visibleUnits])  # Number of unique movies
    hb = tf.placeholder("float", [hiddenUnits])  # Number of features
    W = tf.placeholder("float", [visibleUnits, hiddenUnits])  # Weights that connect the hidden and visible layers

    # Pre-process the input data
    v0 = tf.placeholder("float", [None, visibleUnits])
    _h0 = tf.nn.sigmoid(tf.matmul(v0, W) + hb)
    h0 = tf.nn.relu(tf.sign(_h0 - tf.random_uniform(tf.shape(_h0))))

    # Reconstruct the pre-processed input data (Sigmoid and ReLU activation functions are used)
    _v1 = tf.nn.sigmoid(tf.matmul(h0, tf.transpose(W)) + vb)
    v1 = tf.nn.relu(tf.sign(_v1 - tf.random_uniform(tf.shape(_v1))))
    h1 = tf.nn.sigmoid(tf.matmul(v1, W) + hb)

    # Set RBM training parameters
    alpha = 0.1  # Set learning rate
    w_pos_grad = tf.matmul(tf.transpose(v0), h0)  # Set positive gradients
    w_neg_grad = tf.matmul(tf.transpose(v1), h1)  # Set negative gradients

    # Calculate contrastive divergence to maximize
    CD = (w_pos_grad - w_neg_grad) / tf.to_float(tf.shape(v0)[0])

    # Create methods to update the weights and biases
    update_w = W + alpha * CD
    update_vb = vb + alpha * tf.reduce_mean(v0 - v1, 0)
    update_hb = hb + alpha * tf.reduce_mean(h0 - h1, 0)

    # Set error function (RMSE)
    err = v0 - v1
    err_sum = tf.sqrt(tf.reduce_mean(err * err))

    # Initialize variables
    cur_w = np.zeros([visibleUnits, hiddenUnits], np.float32)  # Current weight
    cur_vb = np.zeros([visibleUnits], np.float32)  # Current visible unit biases
    cur_hb = np.zeros([hiddenUnits], np.float32)  # Current hidden unit biases
    prv_w = np.zeros([visibleUnits, hiddenUnits], np.float32)  # Previous weight
    prv_vb = np.zeros([visibleUnits], np.float32)  # Previous visible unit biases
    prv_hb = np.zeros([hiddenUnits], np.float32)  # Previous hidden unit biases

    return v0, W, vb, hb, update_w, prv_w, prv_vb, prv_hb, update_vb, update_hb, cur_w, cur_vb, cur_hb, err_sum

For my TensorFlow implementation, I designed the RBM architecture with a hidden layer of 100 units activated by a non-linear sigmoid function. Other hyper-parameters include the batch size of 512 and epochs of 50. I also showed a sample recommendation list for a hypothetical user with explainability scores included.

3 — Neural Autoregressive Distribution Estimator for Collaborative Filtering

One of the issues with the RBM model is such that it suffers from inaccuracy and impractically long training time since: (1) training is intractable, and (2) variational approximation or Markov Chain Monte-Carlo is required. Uria, Cote, Gregor, Murray, and Larochelle proposed the so-called Neural Autoregressive Distribution Estimator (NADE), which is a tractable distribution estimator for high-dimensional binary vectors. The estimator computes the conditional probabilities of each element, given the other elements to its left in the binary vector, where all conditionals share the same parameters. The probability of the binary vector can then be obtained by taking the product of these conditionals. NADE can be optimized efficiently via back-propagation, instead of expensive inference required to handle latent variables as in the case of RBM.

As shown in the NADE diagram below:

In the input layer, units with value 0 are shown in black, while units with value 1 are shown in white. The dashed border represents a layer pre-activation.
The outputs x^_0 give predictive probabilities for each dimension of a vector x_0, given elements earlier in some order.
There is no path of connections between an output and the value being predicted, or elements of x_0 later in the ordering.
Arrows connected correspond to connections with shared parameters.

Illustration of a NADE model, as shown in “Neural Autoregressive Distribution Estimation.”

Zheng, Tang, Ding, and Zhou proposed CF-NADE, which is inspired by RBM-CF and NADE models, that models the distribution of user ratings. Suppose we have four movies: m1 (rating is 5), m2 (rating is 3), m3 (rating is 4), and m4 (rating is 2). More specifically, the procedure goes as follows:

The probability that the user gives m1 5-star conditioned on nothing.
The probability that the user gives m2 3-star conditioned on giving m1 5-star.
The probability that the user gives m3 4-star conditioned on giving m1 5-star and m2 3-star.
The probability that the user gives m4 2-star conditioned on giving m1 5-star, m2 3-star, and m3 4-star.

Mathematically speaking, CF-NADE models the joint probability of the rating vector r by the chain rule as:

D is the number of items that the user has rated.
o is the D-tuple in the permutations of (1, 2, …, D).
mᵢ ∈ {1, 2, …, M} is the index of the i-th rated item.
rᵘ = (rᵘ_{m_{o₁}}, rᵘ_{m_{o₂}}, …, rᵘ_{m_{oD}}) denotes the training case for user u.
rᵘ_{m_{oᵢ}} ∈ {1, 2, …, K} denotes the rating that the user gave to item m_{oᵢ}.
rᵘ_{m_{o<ᵢ}} denotes the first i — 1 elements of r indexed by o.

To expand on the process of getting the conditionals in equation 5, CF-NADE first computes the hidden representation of dimension H given rᵘ_{m_{o<ᵢ}} as follows:

g is the activation function.
Wᵏ is the connection matrix associated with rating k.
Wᵏ_{:,j} is the j-th column of Wᵏ and Wᵏ_{i,j} is an interaction parameter between the i-th hidden unit and item j with rating k.
c is the bias term.

Using this hidden representation from equation 6, CF-NADE then computes sᵏ_{m_{oᵢ}} (r_{m_{o_{<i}}}), which is the score indicating the preference that the user gave rating k for item m_{oᵢ}, given the previous ratings r_{m_{o_{<i}}}:

Vʲ and bʲ are the connection matrix and the bias term associated with rating k, respectively, where k is bigger than or equal to j. Using this score from equation 7, the conditionals in equation 5 could be modeled as:

CF-NADE is optimized via minimization of the negative log-likelihood of p(r) in equation 5:

Ideally, the order of movies (represented by notation o) should follow the timestamps of ratings. However, the paper shows that random drawing can yield good performance.

The Keras code of the CF-NADE model class is given below for illustration purpose:

class NADE(Layer):
    def __init__(self, hidden_dim, activation, W_regularizer=None, V_regularizer=None,
                 b_regularizer=None, c_regularizer=None, bias=False, args=None, **kwargs):

        self.init = initializers.get('uniform')

        self.bias = bias
        self.activation = activation
        self.hidden_dim = hidden_dim

        self.W_regularizer = regularizers.get(W_regularizer)
        self.V_regularizer = regularizers.get(V_regularizer)
        self.b_regularizer = regularizers.get(b_regularizer)
        self.c_regularizer = regularizers.get(c_regularizer)

        self.args = args

        super(NADE, self).__init__(**kwargs)

    def build(self, input_shape):
        """
        Build the NADE architecture
        :param input_shape: Shape of the input
        """
        self.input_dim1 = input_shape[1]
        self.input_dim2 = input_shape[2]

        self.W = self.add_weight(shape=(self.input_dim1, self.input_dim2, self.hidden_dim),
                                 initializer=self.init, name='{}_W'.format(self.name), regularizer=self.W_regularizer)

        if self.bias:
            self.c = self.add_weight(shape=(self.hidden_dim,), initializer=self.init,
                                     name='{}_c'.format(self.name), regularizer=self.c_regularizer)

        if self.bias:
            self.b = self.add_weight(shape=(self.input_dim1, self.input_dim2), initializer=self.init,
                                     name='{}_b'.format(self.name), regularizer=self.b_regularizer)

        self.V = self.add_weight(shape=(self.hidden_dim, self.input_dim1, self.input_dim2),
                                 initializer=self.init, name='{}_V'.format(self.name), regularizer=self.V_regularizer)

        super(NADE, self).build(input_shape)

For my Keras implementation, I designed NADE architecture with a hidden layer of 100 units optimized via Adam with a learning rate of 0.001. Other hyper-parameters include the batch size of 512 and epochs of 50.

Model Evaluation

You can check out all three Boltzmann Machines-based recommendation models that I built at this repository: https://github.com/khanhnamle1994/transfer-rec/tree/master/Boltzmann-Machines-Experiments.

The dataset is MovieLens 1M, similar to the three previous experiments that I have done using Matrix Factorization, Multilayer Perceptron, and Autoencoders. The goal is to predict the ratings that a user will give to a movie, in which the ratings are between 1 to 5.
The evaluation metric is Root Mean Squared Error (RMSE) in this setting. In other words, I want to minimize the delta between the predicted rating and the actual rating.
The result table is at the bottom of my repo’s README: the explainable RBM model has the lowest RMSE and shortest training time, while the NADE model has the highest RMSE and longest training time.

Conclusion

In this post, I have discussed the nuts and bolts of Boltzmann Machines and their use in collaborative filtering. I also walked through 3 different papers that use architectures inspired by Boltzmann Machines for the recommendation framework: (1) Restricted Boltzmann Machines, (2) Explainable Restricted Boltzmann Machines, and (3) Neural Autoregressive Distribution Estimator.

There are a couple of other papers worth being mentioned that I haven’t had time to go into details:

Georgiev and Nakov used RBMs to jointly model both: (1) the correlations between a user’s voted items and (2) the correlation between the users who voted a particular item to improve the accuracy of the recommendation system.
Hu et al. used RBM in group-based recommendation systems to model group preferences by jointly modeling collective features and group profiles.
Truyen et al. used Boltzmann machines to extract both: (1) the relation between a rated item and its rating (thanks to the connections between the hidden layer and the softmax layer) and (2) the correlations between rated items (thanks to the connections between the softmax layer units).
Gunawardana and Meek used Boltzmann machines not only for modeling correlation between users and items but also for integrating content information. More specifically, the model parameters are tied with the content information.

Stay tuned for the next blog post of this series that explores the various types of evaluation metrics in the context of recommendation systems.

References

Restricted Boltzmann Machines for Collaborative Filtering. Ruslan Salakhutdinov, Andriy Mnih, and Geoffrey Hinton. June 2007.
Explainable Restricted Boltzmann Machines for Collaborative Filtering. Behnoush Abdollahi and Olfa Nasraoui. June 2016.
A Neural Autoregressive Approach to Collaborative Filtering. Yin Zheng, Bangsheng Tang, Wenkui Ding, and Hanning Zhou. May 2016.