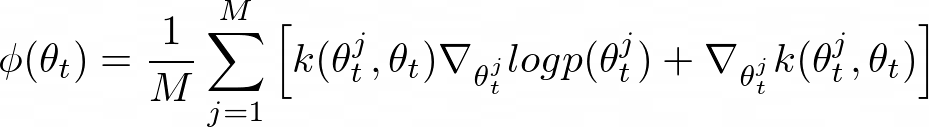In my previous post, “Meta-Learning Is All You Need,” I discussed the motivation for the meta-learning paradigm, explained the mathematical underpinning, and reviewed the three approaches to design a meta-learning algorithm (namely, black-box, optimization-based, and non-parametric).

I also mentioned in the post that there are two views of the meta-learning problem: a deterministic view and a probabilistic view, according to Chelsea Finn.

The deterministic view is straightforward: we take as input a training data set Dᵗʳ, a test data point, and the meta-parameters θ to produce the label corresponding to that test input.
The probabilistic view incorporates Bayesian inference: we perform a maximum likelihood inference over the task-specific parameters ϕᵢ — assuming that we have the training dataset Dᵢᵗʳ and a set of meta-parameters θ.

This blog post is my attempt to demystify the probabilistic view and answer these key questions:

Why is the deterministic view of meta-learning not sufficient?
What is the variational inference?
How can we design neural-based Bayesian meta-learning algorithms?

Note: The content of this post is primarily based on CS330’s lecture 5 on Bayesian meta-learning. It is accessible to the public.

1 — The Downsides Of Deterministic Meta-Learning

Deterministic meta-learning approaches provide us with p(ϕᵢ|Dᵢᵗʳ, θ) — a point estimate of the task-specific parameters ϕᵢ given the training set and the meta-parameters θ. In many situations, we need more than just a point estimate. For example, there are various meta-learning problems that are not entirely determined by their data distribution, as their underlying functions are ambiguous given some prior information. These problems happen in safety-critical domains such as autonomous vehicles and medical imaging, in exploration strategies for meta reinforcement learning, and in active-learning.

In particular, active-learning with meta-learning is potentially a research direction with many industry use cases. Active-learning is valuable in cases where the initial amount of labeled data is small — which frequently happens in the messy real-world. This learning paradigm leverages an existing classifier to decide which unlabeled data points that need to be labeled to improve the existing classifier the most. Previous active-learning methods rely heavily on heuristics such as choosing the data points whose label the model is most uncertain about, choosing the data points whose addition will cause the model to be least uncertain about other data points, or choosing the data points that are different compared to others according to a similarity function.

Figure 1: A summary of the modules in the model shown in “Learning Algorithms for Active Learning.”

Woodward and Finn combine meta-learning with reinforcement learning to learn an active learner. More specifically, the authors considered the online setting of active learning, where the agent is presented with examples in a sequence and must choose whether to label the example or request the correct label. Given the reinforcement learning paradigm, the model is a policy with two actions (labeling and requesting labels) and thus can effectively make decisions with few labeled examples.
Konyushkova et al. introduce a data-driven approach to meta-learning termed Learning Active Learning. Given a trained classifier and its output for a specific example without a label, the authors trained a regressor to predict the reduction in generalization error that can be expected by adding the label to that point. The resulting active learning strategy was then personalized to the specific problem at hand and could be used to further extend to the initial dataset. This query selection strategy outperformed competing methods without requiring hand-crafted heuristics and at a comparatively low computational cost.
Bachman et al. propose a model that learns active learning algorithms via meta-learning (figure 1). The model interacts with labeled items for many related tasks to discover an active learning strategy for the task at hand. This learned active learning strategy could outperform task-agnostic heuristics by sharing experience across associated tasks. In particular, the authors figured out a way to balance the data representation, the active learning strategy, and the prediction function constructor.

We can address the drawbacks of deterministic meta-learning by generating hypotheses about the underlying function, sampling from that data distribution, and reasoning about the model uncertainty. This is where Bayesian meta-learning comes in.

2 — A Light Touch On Bayesian Non-Deep Learning Meta-Learners

Before discussing the meta-learners that utilize deep learning, let us pay respect to the efforts that tackled meta-learning before the neural networks revolution:

Figure 2: Learning a similarity metric for the novel “wildebeest” class based on one example, as illustrated in “One-shot Learning with a Hierarchical Nonparametric Bayesian Model.”

“One-shot Learning of Object Categories” by Fei-Fei, Fergus, and Perona (2006) is one of the earliest approaches that use meta-learning for object recognition tasks. Rather than learning from scratch, the authors took advantage of knowledge coming from previously learned categories, no matter how different these categories might be. This hypothesis was conducted via a Bayesian setting: The authors extracted “general knowledge” from previously learned categories and represented it in the form of a prior probability density function in the space of model parameters. Given a training set, no matter how small, the authors updated this knowledge and produced a posterior density that could be used for object recognition. Their experiments showed that this had been a productive approach and that some useful information about categories could have been obtained from a few training examples.
“One-shot Learning of Simple Visual Concepts” by Lake, Salakhutdinov, Gross, and Tenenbaum (2011) works in the domain of handwritten characters, an ideal setting for studying one-shot learning at the interface of human and machine learning. Handwritten characters contain a rich internal part structure of pen strokes, providing good a priori reason to explore a parts-based approach to representation learning. The authors proposed a new model of character learning based on inducing probabilistic part-based representations. Given an example image of a new character type, the model infers a sequence of latent strokes that best explains the pixels in the image, drawing on a broad stroke vocabulary abstracted from many previous characters. This stroke-based representation guides generalization to new examples of the concept.

“One-shot Learning with a Hierarchical Nonparametric Bayesian Model” by Salakhutdinov, Tenenbaum, and Torralba (2012) leverages higher-order knowledge abstracted from previously learned categories to estimate the new category’s prototype as well as an appropriate similarity metric from just one example. These estimates are also improved as more examples are observed. As illustrated in figure 2, consider how human learners seeing one example of an unfamiliar animal, such as a “wildebeest,” can draw on experience with many examples of “horse,” “cows,” “sheep,” etc. These similar categories have similar prototypes and share similarity variation in their feature-space representations. If we can identify the new example of “wildebeest” as belonging to this “animal” super-category, we can transfer an appropriate similarity metric and thereby generate informatively even from a single example. The algorithm that the authors used is a general-purpose hierarchical Bayesian model that depends minimally on domain-specific representations but instead learns to perform one-shot learning by finding more intelligent representations tuned to specific sub-domains of a task.
“One-shot Learning by Inverting A Compositional Causal Process” by Lake, Salakhutdinov, and Tenenbaum (2013) tackles one-shot learning via a computational approach called Hierarchical Bayesian Program Learning that utilizes the principles of compositionally and causality to build a probabilistic generative model of handwritten characters (figure 3). It is compositional because characters are represented as stochastic motor programs where the primitive structure is shared and reused across characters at multiple levels, including strokes and sub-strokes. Given the raw pixels, the model searches for a “structural description” to explain the image by freely combining these elementary parts and their spatial relations. It is causal because strokes are not modeled at the level of muscle movements, but they are abstract enough to be completed by higher-order actions.

Figure 3: An illustration of the HBPL model generating two character types, where the dotted line separates the type-level from the token-level variables (in “One-shot Learning by Inverting A Compositional Causal Process”) — Figure 3: An illustration of the HBPL model generating two character types, where the dotted line separates the type-level from the token-level variables (in “One-shot Learning by Inverting A Compositional Causal Process”)

3 — A Primer On Bayesian Deep Learning

Deep learning requires a large amount of high-quality data and thus can overfit when the dataset size is small. Other common issues include catastrophic forgetting (the forgetting of past knowledge) and unreliable confidence estimates (lack of robustness and vulnerability to adversarial attacks). Ultimately, due to such issues, real-world applications of deep learning are still challenging.

Bayesian principles have the potential to address such issues:

We can use posterior distribution to represent model uncertainty.
We can use Bayes’ rule to enable sequential learning.
We can use Bayesian model averaging to reduce over-fitting.

Despite these benefits, they are rarely employed in practice due to computational concerns of the posterior distribution, which overshadows their theoretical advantages.

Figure 4: Graphical Model for Deep Latent Gaussian Models, as shown in “Stochastic Back-propagation and Approximate Inference in Deep Generative Models.”

So, what are the different approaches to build neural networks that can measure uncertainty?

A prevalent method is to use latent variable models and optimize them via variational inference. To perform efficient inference and learning in directed probabilistic models, Kingma and Welling introduce a stochastic variational inference and learning algorithm that scales to large datasets and even works in the intractable case. More specifically, the paper comes up with the reparameterization trick to yield a lower bound estimator, which can be used for efficient approximate posterior inference in almost any model with continuous latent variables. Rezende et al. combine ideas from neural networks and probabilistic latent variable modeling to derive a general class of Deep Latent Gaussian models (shown in figure 4), which are principally directed graphical models that consist of Gaussian latent variables at each layer of a processing hierarchy. Furthermore, the paper presents an approach for a scalable variational inference that allows for joint optimization of both variational and model parameters by exploring the properties of latent Gaussian distributions and gradient back-propagation.
Another method is to use an ensemble to estimate the model uncertainty. Lakshminarayanan et al. describe a simple and scalable non-Bayesian method for determining predictive uncertainty estimates from neural networks. The technique uses a combination of ensembles (which captures “model uncertainty” by averaging predictions over multiple models consistent with the training data), and adversarial training (which encourages local smoothness), for robustness to model misspecification and out-of-distribution examples. This method requires minimal hyper-parameter tuning and is well suited for large-scale distributed computation and can be readily implemented for a wide variety of architectures.
The next method is to represent an explicit distribution over the weights of the neural network parameters. Blundell et al. introduce an algorithm called Bayes by Backbrop that learns the weights of neural networks with uncertainty. It optimizes a well-defined objective function to learn a distribution on the weights (shown in figure 5). The paper argues that introducing uncertainty on the weights: (1) helps with regularization via a compression cost on the weights, (2) provides richer representations and predictions from cheap model averaging, and (3) assists with exploration strategies in simple reinforcement learning problems such as contextual bandits.
We can also use normalizing flows: a class of models that attempt to represent a function over a data distribution by (1) inverting some latent distribution into the data distribution or (2) transforming from latent space into the data space and back into the latent space. Dinh et al. propose Non-Linear Independent Component Estimation (NICE), a normalizing flow model type that can model complex high-dimensional densities. Its architecture is capable of learning a highly non-linear bijective transformation (that maps the training data to space where its distribution is factorized) via maximum log-likelihood. The authors also noted that NICE could enable robust approximate inference allowing a complex family of approximate posterior distributions in variational auto-encoders.
Finally, we have energy-based models. Energy-Based models capture dependencies between variables by associating scalar energy to each configuration of the variables. At inference time, we set the value of those observed variables and find the values of the remaining variables that minimize the energy. At training time, we find an energy function that associates low energies to correct values of the remaining variables and higher energies to incorrect values. Because there is no requirement for proper normalization, energy-based approaches avoid the problem associated with estimating the normalization constant in probabilistic models. Furthermore, the absence of the normalization condition allows for much more flexibility in the design of learning machines. Generative adversarial networks are a popular type of energy-based models.

Figure 5: How weights are assigned in classical back-propagation (left) and Bayes by Backprop (right) — as shown in “Weight Uncertainty in Neural Networks.”

4 — A Brief Coverage of Variational Inference

Out of all the methods presented in the previous section, the most progress in Bayesian meta-learning has relied on latent variable models optimized with variational inference. Thus, I want to carve out a section to cover variational inference for the un-initiated briefly.

Figure 6: Graphical model shown in “Auto-Encoding Variational Bayes.” — Figure 6: Graphical model shown in “Auto-Encoding Variational Bayes.”

The graphical model in figure 6 is a typical module in a variational autoencoder (VAE), where z is the latent variable, and x is the observed variable. Given such notations, we want to define the Evidence Lower Bound (ELBO) to estimate a lower bound on the data likelihood such that we can use the likelihood to optimize over a distribution over x.

ELBO includes (1) the expectation with respect to q(z|x) and (2) an entropy term H(q(z|x)) that regularizes over q(z|x). Equation 1 can then be rewritten such that:

The first term on the right-hand side corresponds to the reconstruction loss of the decoder block in a VAE — which is the data likelihood after sampling from the inference network q. The second term on the right-hand side corresponds to the KL divergence between the inference network q and the prior network p. To unpack this further:

p(x|z) is represented by a neural network that takes in the latent variable as inputs and returns their corresponding outputs.
q(z|x) is represented by a neural network that serves the variational distribution of the probability of x and z.
p(z) is represented by a neural network that learns the mean and the variance of the latent variable z.

When using variational inference in the context of meta-learning, θ (meta-parameters) represent the parameters of p and ϕ (task-specific parameters) represent the parameters of q.

An arising issue with this setup is that ELBO contains an expectation with respect to q, meaning that we need to be able to back-propagate into the q distribution. However, sampling is not differentiable. Thankfully, we have the reparametrization trick! This trick represents q(z|x) in a differentiable way in terms of the noise that is sampled from a Gaussian unit:

More specifically, if the Gaussian distribution of the latent variable z corresponds to the output of the neural network q, then we can represent the output of q as being re-parametrized by the mean (μ) plus the variance (σ) times the noise (ϵ). If the inference network q is expressive enough, it can easily represent a Gaussian distribution over latent variables z. This process is often known as amortized variational inference, as we amortize the process of estimating the variational distribution that needs to be predicted by our inference network.

So how can we use amortized variational inference for meta-learning?

5 — Bayesian Black-Box Meta-Learners

Recall the explanation of black-box meta-learning in my previous post; we have a neural network that takes a training dataset as input and produces a distribution over task-specific parameters ϕ as outputs. Then, we apply task-specific parameters ϕ to parametrize a neural network that takes feature set x as input and produces labels y as output. Essentially, we want to maximize the test data likelihood yᵗˢ given task-specific parameters ϕ, given that ϕ are sampled as a function of training set Dᵗʳ.

In the case of meta-learning, we can apply ELBO such that the observed variable is the dataset D, and the latent variable is the task-specific parameters ϕ. The form of equation 4 mirrors the shape of equation 2.

The inference network q captures a variational distribution over the task-specific parameters ϕ, where we sample from and estimate the data likelihood given ϕ (p(D|ϕ)). The KL divergence term indicates that the variational distribution and the prior over ϕ must be similar (D_KL (q(ϕ) || p(ϕ))).

What should we condition our inference network q on?

First, to sample the task-specific parameters ϕ as a function of the data, we need to condition q on the training set Dᵗʳ. Equation 4 becomes:

Second, to maximize the likelihood of test data points yᵗˢ given task-specific parameters ϕ, we need to sample ϕ as a function of Dᵗʳ.

What should we condition our meta-parameters θ on?

There are two changes we can make to equation 6:

We make the prior p(ϕ) to be conditioned on θ.
We make the inference network q(ϕ | Dᵗʳ) to be conditioned on θ.

Finally, we want to perform maximum likelihood with respect to the meta-parameters θ and expectations over all of the tasks (Tᵢ is a sample task, and i is the current iteration). The KL divergence term encourages the inference network q to stay close to the prior distribution p.

What are the papers that use Bayesian Black-Box Meta-Learning to read up on?

“Towards a Neural Statistician” by Edwards and Storkey presents a statistic network that takes as input a set of vectors and outputs a vector of summary statistics specifying a generative model of that set — a mean and a variance determining a Gaussian distribution in a latent space. The approach is unsupervised, data-efficient, and parameter-efficient. In terms of meta-learning capability, if the datasets correspond to examples from different classes, class embeddings (summary statistics associated with examples form a class) allow the network to handle new classes at test time.
“Conditional Neural Processes” by Garnelo et al. proposes a family of neural models that are inspired by the flexibility of Gaussian Processes (a Bayesian method), but is structured as neural networks and trained via gradient descent. While most conventional deep learning models can only learn functions that are tied to a constrained statistical context at any stage of training, Conditional Neural Processes can encapsulate the high-level statistics of a family of functions. As such, it constitutes a high-level abstraction that can be reused for multiple tasks.
“Meta-Learning Probabilistic Inference for Prediction” by Gordon et al. devises ML-PIP, a probabilistic framework for meta-learning that incorporates three key elements. First, it leverages a shared statistical structure between tasks via hierarchical probabilistic models developed for multi-task learning and transfer learning. Second, it shares information between tasks about how to learn and perform inference during meta-learning. Third, it enables fast learning that can flexibly handle a wide range of tasks and learning settings via amortization. Building on top of this framework, the paper showcases VERSA (figure 7) — which substitutes optimization procedures at test time with forwarding passes through inference networks. This process amortizes the inference cost and relieves the need for second derivatives during training. Concretely speaking, VERSA uses a flexible amortization network that takes meta-learning datasets and produces a probability distribution over task-specific parameters in a single forward pass.

Figure 7: Computational flow of VERSA for few-shot classifications with the context-independent approximation — as presented in “Meta-Learning Probabilistic Inference for Prediction.”

Summary

The benefits of Bayesian black-box meta-learning methods include their capacity to: (1) represent non-Gaussian distributions over test labels yᵗˢ, and (2) represent distributions over task-specific parameters ϕ. Thus, we can represent uncertainty over the underlying function and not just the underlying data points.
The downside is that they can only represent the Gaussian distribution p(ϕᵢ | θ) because: (1) reparametrization trick only holds for Gaussian, and (2) the KL divergence term can be evaluated in closed form for Gaussian objectives, but cannot be evaluated in closed form for other non-Gaussian objectives.

6 — Bayesian Optimization-Based Meta-Learners

6.1 — Recasting MAML as Hierarchical Bayes

Figure 8: The probabilistic graphical model for which MAML provides an inference procedure as described in “Recasting Gradient-Based Meta-Learning as Hierarchical Bayes.”

In my previous post Meta-Learning Is All You Need, I pointed out that we can recast gradient-based meta-learning as hierarchical Bayes. Grant et al. provide a Model-Agnostic Meta-Learning (MAML) formulation as a method for probabilistic inference via hierarchical Bayes (recall that MAML is the original optimization-based meta-learning model). Let’s say we have a graphical model, as illustrated in figure 8, where J is the task, x_{j_n} is a data point in that task, ϕⱼ are the task-specific parameters, and θ represents the meta-parameters.

To perform inference with respect to this graphical model, we want to maximize the likelihood of the data given the meta-parameters:

The probability of the data given the meta-parameters can be expanded into the probability of the data given the task-specific parameters and the probability of the task-specific parameters given the meta-parameters. Thus, equation 9 can be rewritten in an empirical Bayes fashion as:

This integral in equation 10 can be approximated with a Maximum a Posteriori (MAP) estimate for ϕⱼ:

This is nice in the sense that it provides a Bayesian interpretation of MAML as a way to learn meta-parameters θ — such that during test time, we perform MAP inference under a Gaussian prior represented by meta-parameters ϕᵢ. As pointed out in equation 11, this method represents a point estimate of the full distribution and only gives one set of parameters for this distribution. Therefore, we cannot sample from the entire distribution of our task-specific parameters p(ϕᵢ| θ, Dᵢᵗʳ).

6.2 — Amortized Bayesian MAML

To address such an issue, we can build upon what we derived from Bayesian black-box meta-learning, as displayed in equation 8. In particular, the inference network q can be any arbitrary function. Ravi and Beatson bring amortized variational inference to MAML by including a gradient operator to q. Here q is represented by the local variational parameters λᵢ produced after K steps of gradient descent on the loss for the training set Dᵢᵗʳ, starting from the global initialization θ:

Note here that θ serves as both the global initialization of local variational parameters and the parameters of the prior p(ϕ | θ). With this form of the variational distribution, we run gradient descent with respect to the mean and the variance of a set of parameters with respect to some training data.

Thus, a significant benefit is that we get both the mean and the variance of the full distribution of our task-specific parameters p(ϕᵢ| θ, Dᵢᵗʳ) during test time. The paper shows that only a few steps of gradient descent are required to produce a stable local variational distribution for any given dataset.
However, a downside (similar to Bayesian black-box meta-learning) is that p(ϕᵢ| θ, Dᵢᵗʳ) can only be modeled as a Gaussian posterior distribution.

6.3 — Bayesian MAML

A logical step up is then to be able to model non-Gaussian posterior distribution. Kim et al. present Bayesian Model-Agnostic Meta-Learning (Bayesian MAML) that uses a variation on the MAML algorithm to accelerate a robust Bayesian Neural Network. The authors noticed that an important algorithm for training a Bayesian Net, Stein Variational Gradient Descent (SVGD), is theoretically compatible with gradient-based meta-learning. SVGD, proposed by Liu & Wang, is a non-parametric variational inference algorithm that combines the strengths of Markov Chain Monte-Carlo and variational inference. SVGD uses a set of particles for approximation, on which a form of functional gradient descent is performed to minimize the KL divergence and drive the particles to fit the true posterior distribution.

Specifically, to obtain M samples from target distribution p(θ), SVGD maintains M instances of model parameters, called particles. At iteration t, each particle θt is updated by the following rule (where ϵt is the step size):

Then Bayesian MAML uses SVGD to push particles away from one another (where k(x, x’) is a positive-definite kernel):

Equation 14 confirms that a particle consults with other particles by asking their gradients and determining its update direction. The importance of other particles is weighted according to the kernel distance, relying more on closer particles. The last term ∇_{θtʲ} k(θtʲ, θt) enforces repulsive force between particles so that they do not collapse to a point.

As you can see, the SVGD algorithm has a simple mechanism and can be applied in any case of gradient descent. Indeed, it reduces to gradient descent for MAP when using only a single particle, while turns into a fully Bayesian approach with more particles.

Figure 9: Fast careful adaptation with Bayesian MAML by Element AI — Figure 9: Fast careful adaptation with Bayesian MAML by Element AI

Furthermore, instead of just pushing the particles away from another, Bayesian MAML learns to infer by developing an efficient Bayesian gradient-based meta-learning method to efficiently obtain the task-posterior p(θ_k | D_kᵗʳ) of a new task k (called Bayesian Fast Adaptation as seen in figure 9). This method can be considered a Bayesian ensemble in which, unlike non-Bayesian ensemble methods, the particles interact with each other to find the best formation representing the task-train posterior.

Specifically, at iteration t, for task k in a sampled mini-batch T_k, the particles initialized to Θ₀ are updated for n steps by applying the SVGD updater. This results in task-wise particles Θ_k for each task k ∈ T_k. Then, for the meta-update, we can use the following meta-loss:

Here, Bayesian MAML uses Θ_k (Θ₀) to denote that Θ_k is a function of Θ₀ explicitly. The Bayesian Fast Adaptation (BFA) loss is optimized for distribution of M particles to produce high likelihood:

All the initial particles in Θ₀ are jointly updated to find the best join-formation among them. From this optimized initial particles, the task-posterior of a new task can be obtained quickly (by taking a small number of update steps) and efficiently (with a small number of samples).

The benefits of Bayesian MAML include its simple mechanism, its high efficiency, and its capability to model non-Gaussian posterior distribution.
The downsides are that we need to maintain M model instances, and we can only perform gradient-based inference only on the last layer.

Can we model non-Gaussian posterior distributions over all the meta parameters without maintaining separate model instances?

6.4 — Probabilistic MAML

Finn, Xu, and Levine design Probabilistic Model-Agnostic Meta-Learning, which extends MAML to model a distribution over prior model parameters via a simple stochastic adaptation procedure that injects noise into gradient descent at meta-test time. The meta-training procedure optimizes this inference process to produce samples from an approximate model posterior.

In particular, we have the original graphical model, as shown in figure 10 (left), where tasks are indexed over i and data points are indexed over j. We want a hierarchical Bayesian model that includes random variables for the prior distribution over meta parameters θ, the distribution over task-specific parameters ϕᵢ, and the task training/test data points. We can get the predictions for each task by sampling ϕᵢ, which are influenced by the prior p(ϕᵢ | θ) and the observed training data (xᵗʳ, yᵗʳ).

The posterior on ϕᵢ can be expanded in an empirical Bayes fashion (as suggested in Grant et al.):

In the case of non-Gaussian likelihoods, the equivalence is only locally approximate, and the exact solution for this distribution is completely intractable. To address this issue, Probabilistic MAML approximates it with Maximum a Posteriori (MAP) using a point estimate for ϕ:

In particular, ϕ^ᵢ is obtained via gradient descent on the training set starting from θ:

Although this is a crude approximation to the likelihood, equation 19 provides an empirically effective and straightforward tool to simplify the variational inference procedure. The original graphical model is transformed into the one shown in figure 10 (center). In this new graphical model, the meta parameters θ are independent of all observed variables xᵗʳ, yᵗʳ, and xᵗˢ.

Figure 10: Graphical Models corresponding to Probabilistic Model-Agnostic Meta-Learning — Figure 10: Graphical Models corresponding to Probabilistic Model-Agnostic Meta-Learning

In this instance, the variational lower bound for the logarithm of the approximate likelihood is given by:

With this bound, we perform approximate inference via MAP on ϕᵢ to obtain p(ϕᵢ|xᵢᵗʳ, yᵢᵗʳ, θ) (equation 19) and use the variational distribution for θ only. The inference network q_{ψ} is used for all tasks and is defined by the below function approximator with parameters ψ that takes xᵢᵗʳ, yᵢᵗʳ as input:

In equation 22, μ_θ is the learned mean and v_q is the learned diagonal covariance of the prior p(θ), while γ_q is a learning rate “vector” that is point-wise multiplied with the gradient.

During training, Probabilistic MAML uses the ancestral sampling procedure to evaluate the above variational lower bound (equation 21):

First, we evaluate the mean by starting from μ_θ and taking one (or more) gradient steps on log p(yᵢᵗˢ|xᵢᵗˢ, θₐ), where θₐ starts at μ_θ.
Second, we add noise with variance v_q, which is differentiable thanks to the reparametrization trick.
Third, we take additional gradient steps on the training likelihood log p(yᵢᵗʳ|xᵢᵗʳ, θₐ), which corresponds to performing MAP inference on ϕᵢ.
Finally, we execute back-propagation through the whole procedure with respect to the variational lower bound. The parameters μ_θ, γ_θ², and v_q are updated along the way.

During inference, Probabilistic MAML sample θ and perform MAP inference on ϕᵢ using the training set.

The benefits of Probabilistic MAML are such that it can capture non-Gaussian posterior, and it only requires one model instance (in contrast to Bayesian MAML).
The downside is that it requires a more complex training procedure.

Summary

For Bayesian optimization-based meta-learning methods, I brought up three types: amortized inference, an ensemble of MAML, and hybrid inference.

Amortized Bayesian MAML is simple to implement, but it can only model p(ϕᵢ | θ) as a Gaussian objective (same issue with that of Bayesian black-box methods).
Bayesian MAML also has a simple mechanism and tends to work decently well. This approach can model non-Gaussian distribution but needs to maintain separate model instances.
Probabilistic MAML with the hybrid inference approach can model non-Gaussian distribution and has only one model instance. However, it has quite a complicated training procedure.

7 — Conclusion

In this post, I have discussed the motivation for Bayesian meta-learning, the historical Bayesian non-neural-based meta-learners, the intuition behind variational inference, as well as the two approaches regarding the design of Bayesian meta-learning algorithms. In particular:

Bayesian black-box meta-learning algorithms use latent variable models alongside amortized variational inference. The significant benefit is that they can represent all types of distributions over test labels yᵗˢ, but they can only represent p(ϕᵢ | θ) as Gaussian distribution.
Bayesian optimization-based meta-learning algorithms include three different methods: amortized Bayesian MAML, Bayesian MAML, and Probabilistic MAML. Their pros and cons are discussed above — where Bayesian MAML and Probabilistic MAML are preferred approaches.

Stay tuned for part 3 of this series, where I’ll go over Unsupervised Meta-Learning!