Introduction

In my previous posts, “Meta-Learning Is All You Need” and “Bayesian Meta-Learning Is All You Need,” we have only discussed meta-learning in the supervised setting, in which we have access to labeled data and hand-specified task distributions. However, acquiring labeled data for many tasks and manually constructing task distributions is challenging and time-consuming. Such dependencies put conceptual limits on the type of problems that can be solved through meta-learning.

Can we design a meta-learning algorithm to handle unlabeled data, where the algorithm can come up with its own tasks that prepare for future downstream tasks?

Unsupervised meta-learning algorithms effectively use unlabeled data to tune their learning procedures by proposing their task distributions. A robust unsupervised meta-learner, once trained, should be able to take new and different data from a task with labels, acquire task-specific knowledge from the training set, and generalize well on the test set during inference.

This blog post is my attempt to explore the unsupervised lens of meta-learning and tackle the most prominent papers in this sub-domain.

1 — CACTUs

Hsu, Levine, and Finn come up with Clustering to Automatically Construct Tasks for Unsupervised Meta-Learning (CACTUs) — an unsupervised meta-learning method that learns a learning procedure, without supervision, that is useful to solve a wide range of new human-specified tasks. With only raw unlabeled observations, the model can learn a reasonable prior such that, after meta-training, when presented with a small dataset for a human-specified task, the model can transfer its previous experience to learn to perform the new task efficiently.

The diagram below illustrates CACTUs:

Given raw unlabeled images, the algorithm first runs unsupervised learning on the images to get a low-dimensional embedding space.
Second, the algorithm proposes tasks by clustering the embeddings multiple times within this low-dimensional latent space. Different data groupings will then be generated. To get a task, the algorithm samples these different groupings and treat each grouping as a separate class label.
Third, the algorithm runs meta-learning methods (black-box, optimization-based, or non-parametric) on the tasks. The result of this process is going to be a representation that is suitable for learning downstream tasks.

The CACTUs method, as proposed in “Unsupervised Learning via Meta-Learning.”

Let’s unpack CACTUs further: The key question is how to construct classification tasks from unlabeled data D = {xᵢ} automatically.

CACTUs use k-means clustering to group data points into consistent and distinct subsets based on salient features. If the clusters can recover a semblance of the true class-conditional generative distributions, creating tasks based on treating these clusters as classes should result in useful unsupervised meta-learning. However, the result of k-means is critically dependent on the metric space on which its objective is defined. Thus, CACTUs use SOTA unsupervised learning methods to produce useful embedding spaces. In particular, the authors try out four different embedding methods to generate tasks: ACAI, BiGAN, DeepCluster, and InfoGAN.

Adversarially Constrained Autoencoder Interpolation (ACAI) is a convolutional autoencoder architecture whose loss is regularized with a term that encourages meaningful interpolations in the latent space.
Bidirectional GAN (BiGAN) is a generative adversarial network where the discriminator produces synthetic images from real embedding and synthetic embedding from real image.
DeepCluster is a clustering technique where: first, the features of a convolutional neural network are clustered. Second, the feature clusters are used as labels to optimize the network weights via backpropagation.
InfoGAN is another generative adversarial network where the input to the generator is decomposed into a latent code incompressible noise.

CACTUs run out-of-the-box unsupervised embedding learning algorithms on D, then map the data {xᵢ} into the embedding space Z, producing {zᵢ}. To build a diverse task set, CACTUs generates P partitions {Pₚ} by running clustering P times, applying random scaling to the dimensions of Z to induce a different metric, represented by a diagonal matrix A, for each run of clustering. With μ_c denoting the learned centroid of cluster C_c, a single run of clustering can be summarized with:

With the partitions being constructed over {zᵢ}, CACTUs finally meta-learn on the images, so that the learning procedure can adapt to each evaluation task from the rawest level of representation. For this meta-learning phase, the authors try out two different methods to learn the representation: MAML and ProtoNets.

Model-Agnostic Meta-Learning (MAML) learns the meta-parameters of a neural network so that they can lead to useful generalization in a few gradient steps.
Prototypical Networks (ProtoNets) learn a representation where each class can be effectively identified by its prototype — which is the mean of the class’ training examples in the meta-learned space.

Here are the main benefits of CACTUs from the experimental setting conducted in the paper on MNIST, CelebA, Omniglot, and Mini-ImageNet datasets:

There is a big advantage of meta-learning on tasks derived from embeddings, rather than using only the embeddings for downstream supervised learning of new tasks.
CACTUs is sufficient for all four embedding learning methods that generate tasks.
CACTU learns an effective prior to a variety of task types. This means that it is suitable for tasks with different supervision signals, or tasks that deal with features in different scales.

However, the authors noted that with its evaluation-agnostic task generation, CACTUs trades off performance in specific use cases for broad applicability and the ability to train on unlabeled data. An exciting direction for future work is making CACTUs more robust towards highly unstructured and unlabeled datasets.

2 — UMTRA (2018)

Khodadadeh, Boloni, and Shah present Unsupervised Meta-Learning with Tasks constructed by Random Sampling and Augmentation (UMTRA), which performs meta-learning of one-shot and few-shot classifiers in an unsupervised manner on an unlabeled dataset. As seen in the diagram below:

UMTRA starts with a collection of unlabeled data. The objects within this collection have to be drawn from the same distribution as the objects classified in the target task. Furthermore, the unlabeled data must have a set of classes significantly larger than the number of classes of the final classifier.
Starting from this unlabeled dataset, UMTRA uses statistical diversity properties and domain-specific augmentation to generate the training and validation data for a collection of synthetic tasks.
These tasks are then used in the meta-learning process based on a modified classification variant of the Model-Agnostic Meta-Learning (MAML) algorithm.

The UMTRA method, as proposed in “Unsupervised Meta-Learning for Few-Shot Image Classification.”

More formally speaking:

In supervised meta-learning, we have access to a collection of tasks T₁, …, T, drawn from a specific distribution, with both supervised training and validation data. Each task T has N classes of K training/validation samples.
In unsupervised meta-learning, we don’t have the collection of tasks T₁, …, T, and their associated labeled training data. Instead, we only have an unlabeled dataset U = { … xᵢ …}, with samples drawn from the same distribution as the target task. Every element of this dataset is associated with a natural class C₁ … Cc.

To run the UMTRA algorithm, we need to create tasks Tᵢ from the unsupervised data that can serve the same role as the meta-learning tasks in the full MAML algorithm. For such a task, we need to create both the training data D and the validation data D’.

The training data is Dᵢ = {(x₁, 1), …, (x_N, N)} with xᵢ sampled randomly from U.
The validation data Dᵢ’ = {(x₁’, 1), …, (x_N’, N)} is created by augmenting the sampled used in the training data using an augmentation function xᵢ’ = A(xᵢ).

Experiments on Omniglot and Mini-ImageNet datasets in the paper show that UMTRA outperforms learning-from-scratch approaches and approaches based on unsupervised representation learning. Furthermore, the statistical sampling and augmentation performed by UMTRA can be seen as a cheaper alternative to the dataset-wide clustering performed by CACTUs.

3 — Unsupervised Meta-Reinforcement Learning (2018)

Throughout this series, I haven’t brought up meta reinforcement learning yet, a family of algorithms that can learn to solve new reinforcement learning tasks more quickly through experience on past tasks. They assume the ability to sample from a pre-specified task distribution. They can solve new tasks drawn from this distribution very quickly. However, specifying a task distribution is tedious and requires a significant amount of supervision that may be difficult to provide for sizeable real-world problem settings. Can we automate the process of task design and remove the need for human supervision entirely?

Gupta, Eysenbach, Finn, and Levine apply unsupervised meta-learning to the context of meta reinforcement learning: meta-learning from a task distribution that is acquired automatically, rather than requiring manual design of the meta-training tasks. Given an environment, they want to propose tasks in an unsupervised way and then run meta-reinforcement learning on those tasks. The result is a reinforcement learning algorithm that is tuned for the given environment. Then for that environment, given a reward function from the human, the algorithm can maximize the function with a small amount of experience.

The learning procedure, as shown in “Unsupervised Meta-Reinforcement Learning.”

Formally speaking, the meta-training setting is a controlled Markov process (CMP) — a Markov decision process without a reward function: C = (S, A, P, γ, p) — where S is the state space, A is the action space, P is the transition dynamics, γ is the discount factor, and p is the initial state distribution. The CMP produces a Markov decision process M = (S, A, P, γ, p, r) — where r is the reward function.

f: D -> π is a learning algorithm that inputs a dataset of experience from the MDP (D) and outputs a policy π. This algorithm is evaluated over several episodes: wherein each episode i, f observes all previous data {T₁, …, Tᵢ₋₁} and outputs a policy to be used in iteration i.

The goal of unsupervised meta-reinforcement learning is to take this CMP and produce an environment-specific learning algorithm f that can quickly learn an optimal policy πᵣ* for any reward function r.

The key question is how to propose relevant tasks. The paper attempts to make a set of tasks that are more diverse from each other, where the skills within tasks are entirely different from one another. To cluster skills into discrete parts of the policy space, the authors use Diversity Is All You Need, which is a method that learns skills by maximizing an information-theoretic objective using a maximum entropy policy:

The Pseudocode in “Unsupervised Meta-Reinforcement Learning”

The agent/policy takes as input a discrete skill (z) to produce actions. This skill z is used to generate the states in a given rollout according to a latent-conditioned policy π(a | s, z).
The discriminator network D_{θ} takes as input a state (s) and predicts which skill (z) to be passed into the policy. Diversity Is All You Need enforces a co-operative game where the policy visits which states are discriminable by the discriminator and the discriminator predicts the skill from the state. The objective of both is to maximize the accuracy of the discriminator.
Using the discriminator, the authors make the reward function for unsupervised meta-learning to simply be the likelihood of one of the skills given the state: r_z(s, a) = log (D_{θ} (z|s)).
Then, the authors use MAML with this reward r_z to acquire a fast learning algorithm f to learn new tasks quickly for the current reinforcement learning setting.

In their experiments, the author study three simulated environments of varying difficulty: 2D point navigation, 2D locomotion, and 3D locomotion. The results indicate that unsupervised meta-reinforcement learning effectively acquires accelerated reinforcement learning procedures without manual task design. These procedures exceed the performance of learning from scratch. However, one limitation is that the paper only considers deterministic dynamics and only considers task distributions with optimal posterior sampling. Thus, two exciting directions for future work are experimenting with stochastic dynamics and more realistic task distributions in large-scale datasets and complex tasks.

4 — Assume, Augment, and Learn (2019)

Antoniou and Storkey propose Assume, Augment, and Learn (AAL) that leverages unsupervised data to generate tasks for few-shot learners. This method is inspired by the ability of humans to find features that can accurately describe a set of randomly clustered data points, even when the clusters are continuously randomly reset. The authors believe that bringing this setting to meta-learning can produce strong representations for the task at hand.

The paper uses three separate datasets: a meta-training, a meta-validation, and a meta-test set.

The meta-training set does not have any labels and is used to train a few-shot learner using AAL.
The meta-validation and meta-test sets have labeled data and are used to evaluate the few-shot tasks. Using a validation set to pick the best-trained model and a test set to produce the final test errors removes any potential unintended over-fitting.
Training meta-learning models requires using a large number of tasks. In particular, AAL relies on the set-to-set few-shot learning scheme in Vinyals et al. — where a task is composed of a support (training) set and a target (validation) set. Both sets have a different number of classes but a similar number of samples per class.
Put that into the context of a meta-learning setting: Given a task, AAL learns a model that can acquire task-specific knowledge from the support set to perform well in the target set, before throwing away that knowledge.

The proposed method in “Assume, Augment and Learn: Unsupervised Few-Shot Meta-Learning via Random Labels and Data Augmentation.”

AAL attempts to explore the semantic similarities between data points to learn robust across-task representations that can then be used in a setting where supervised labels are available. It consists of three phases:

First, AAL assumes data labels by randomly assigning labels for a randomly sampled set of data points. This allows the model to acquire fast-knowledge in its parameters that can classify the support set well.
Second, AAL augments the number of data points in the support set via data augmentation techniques. This sets the number of classes in the support set to match the number of classes in the target set. Still, the samples in the two sets are different enough to allow the target set to serve as a satisfactory evaluation set.
Third, AAL learns the tasks via any existing few-shot meta-learning technique, as long as the method can be trained using the set-to-set few-shot learning framework. In the paper, the authors experiment with Model Agnostic Meta-Learning and Prototypical Networks.

Experiments on Omniglot and Mini-ImageNet datasets in the paper verify that AAL generalizes well to real-labeled inference tasks. However, its performance heavily depends on the data augmentation strategies employed. Thus, a future direction would be to automate the search for an optimal data augmentation function to produce fully unsupervised systems with a strong performance.

The papers discussed above all have a common attribute: the meta-objective of the outer loop is unsupervised, and therefore the learner itself is learned without any labels available. As I researched the meta-learning literature, I found another variant of meta-learning that involves unsupervised learning.

In this second variant, meta-learning is used as a means to learn an unsupervised inner loop task. The outer objective in this case can be anything from supervised, unsupervised, or reinforcement-based. This variant can be referred to as Meta-Learning Unsupervised Learning.

5 — Unsupervised Update Rules (2018)

Metz, Maheswaranathan, Cheung, and Sohl-Dickstein present the first meta-learning approach that tackles unsupervised representation learning, where the inner loop consists of unsupervised learning. The paper proposes to meta-learn an unsupervised update rule by meta-training on a meta-objective that directly optimizes the utility of the unsupervised representation. Unlike hand-designed unsupervised learning rules, this meta-objective directly targets the usefulness of a representation generated from unlabeled data for later supervised tasks. This approach contrasts with transfer learning, where a neural network is instead trained on a similar dataset, and then fine-tuned or post-processed on the target dataset.

Furthermore, this is the first representation meta-learning approach to generalize across input data modalities and datasets, the first to generalize across permutation of the input dimensions, and the first to generalize across neural network architectures.

The diagram below provides a schematic illustration of the model:

The left-hand side shows how to meta-learn an unsupervised learning algorithm. The inner loop computation consists of iteratively applying the UnsupervisedUpdate to a base model. During meta-training, the UnsupervisedUpdate (parametrized by θ) is itself updated by gradient descent on the MetaObjective.
The right-hand side goes deeper into the based model and UnsupervisedUpdate. Unlabeled input data (x) is passed through the base model, which is parameterized by W and colored green. The goal of the UnsupervisedUpdate is to modify W to achieve a top layer representation x^L, which performs well at few-shot learning. To train the base model, information is propagated backward by the UnsupervisedUpdate analogous to back-prop (colored blue).

The approach described in “Meta-Learning Update Rules for Unsupervised Representation Learning.”

Let’s take a look at the design of the model deeper.

The base model is a standard fully-connected Multi-Layer Perceptron coupled with batch normalization layers and the ReLU activation unit.
The learned update rule is unique to each neuron layer so that the weight updates are a function of pre- and post-synaptic neurons in the base model and can be defined for any base model architecture. This design enables the update rule to generalize across architectures with different widths, depths, and network topologies.
The meta-objective determines the quality of the unsupervised representations. It is based on fitting a linear regression to labeled examples with a small number of data points.

Based on the experiments on various datasets such as CIFAR 10, MNIST, Fashion MNIST, and IMDB, the performance of this method either matched or exceeded existing unsupervised learning on few-shot image classification and text classification tasks. With no explicitly defined objective, this work is a proof of an algorithm design principle that replaces manual fine-tuning with architectures designed for learning and learned from data via meta-learning.

6 — Meta-Learning For Semi-Supervised Learning (2018)

Ren, Triantafillou, Ravi, Snell, Swersky, Tenenbaum, Larochelle, and Zemel aim to generalize a few-shot learning setup for semi-supervised classification in two ways:

They consider a scenario where the new classes are learned in the presence of additional unlabeled data.
They also consider the situation where the new classes to be learned are not viewed in isolation. Instead, many of the unlabeled examples are from different classes; the presence of such distractor classes introduces an additional and more realistic level of difficulty to the few-shot problem.

The figure below shows a visualization of training and test episodes in the semi-supervised setting:

The training set is a tuple of labeled and unlabeled examples: (S, R).
The labeled examples are called the support set S that contains a list of tuples of inputs and targets.
The unlabeled examples are called the unlabeled set R that contains only the inputs: R = {x₁, x₂, …, x_m}.
The models are trained to perform well when predicting the labels for the examples in the episode’s query set Q.

Example of the semi-supervised few-shot learning setup as described in “Meta-Learning for Semi-Supervised Few-Shot Classification.”

This paper proposes three novel extensions of Prototypical Networks, a SOTA approach to few-shot learning, to the semi-supervised setting. More precisely, Prototypical Nets learn an embedding function h(x), parameterized as a neural network, that maps examples into space where examples from the same class are close and those from different classes are far.

To compute the prototype p_c of each class c, Prototypical Nets average the embedded examples per-class:

These prototypes define a predictor for the class of any query example x*, which assigns a probability over any class c based on the distance between x* and each prototype, as follows:

The loss function used to update Prototypical Networks for a given training episode is simply the average negative log-probability of the correct class assignments, for all query examples:

Training includes minimizing the average loss, iterating over training episodes, and performing a gradient descent update.

In the original formulation, Prototypical Networks (seen in the left side of the figure below) do not specify a way to leverage the unlabeled set R. The extensions start from the basic definition of prototypes and provide a procedure to produce refined prototypes (seen in the right side of the figure below) using the unlabeled examples in R.

After the refined prototypes are generated, each query example is classified into one of the N classes based on the proximity of its embedded position with corresponding refined prototypes. During training, the authors optimize the average negative log-probability of the correct classification.

The prototypical networks before and after refinement, as displayed in “Meta-Learning for Semi-Supervised Few-Shot Classification.”

The first extension was borrowed from the inference performed by soft k-means.

The regular Prototypical Network’s prototypes p_c are used as the cluster locations.
Then, the unlabeled examples get a partial assignment to each cluster based on their Euclidean distance to the cluster locations.
Finally, refined prototypes are obtained by incorporating these unlabeled examples.

The partial assignment is defined as follows:

The extension above assumes that each unlabeled example belongs to either one of the N classes in the episode. However, it would be more general not to make that assumption and have a model robust to the existence of examples from other classes, termed distractor classes.

The second extension added cluster to the assignment, whose purpose is to capture the distractors, thus preventing them from polluting the clusters of the classes of interest:

The third extension incorporated a soft-masking mechanism on the contributions of unlabeled examples. The idea is to make the unlabeled examples that are closer to a prototype to be masked less than those that are farther:

First, normalized distances d_{j,c} are computed between examples xⱼ and prototypes p_c.
Then, soft thresholds β_c and slopes γ_c are predicted for each prototype by feeding a small neural network various statistics of the normalized distances for the prototype.
Finally, soft masks m_{j, c} for the contribution of each example to each prototype are computed by comparing to the threshold the normalized distances.

The refined prototypes are obtained as follows:

From the experiments conducted on Omniglot, miniImageNet, and tieredImageNet, these extensions of Prototypical Networks showed consistent improvements under semi-supervised settings compared to their baselines. For future work, the authors want to incorporate fast weights into their framework so that examples can have different embedding representations given the contents in the episode.

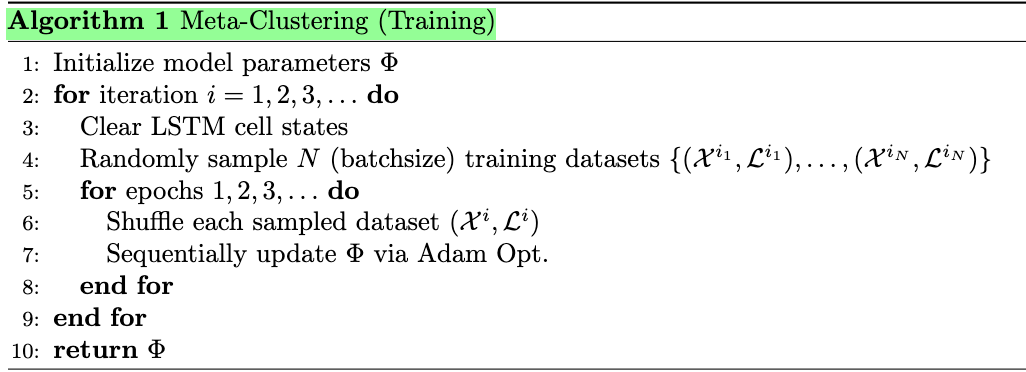
7 — Meta-Clustering (2019)

Jiang and Verma propose a simple yet highly effective meta-learning model to solve for clustering tasks. The model, called Meta-Clustering, finds the cluster structure directly without having to choose a specific cluster loss for each new clustering problem. There are two key challenges in training such a model for clustering:

Since clustering is fundamentally an unsupervised task, true cluster identities for each training task don’t exist.
The cluster label for each new data point depends upon the labels assigned to other data points in the same clustering task.

To address these issues, the authors:

Train their algorithm on simple synthetically generated datasets or other real-world labeled datasets with similar characteristics to generalize to real previously unseen datasets.
Use a recurrent network (LSTMs) and train it sequentially to assign clustering labels effectively based on previously seen data points.

The problem is formally defined as follows: A meta-clustering model M maps data points to cluster labels. The model is trained to adapt to a set of clustering tasks {Tᵢ}. At the end of meta-training, M would produce clustering labels for new test tasks T_test.

Each training task Tᵢ consists of a set of data points X_i and their associated cluster labels L_i.
X_i and L_i are partitioned into subsets based on cluster identities.
The structure of the test task T_test is different from training and consists of only a set of data points X_test.

LSTM Architecture of Meta-Clustering as proposed in “Meta-Learning to Cluster.”

As seen above, Meta-Clustering uses a Long-Short Term Memory (LSTM) network to capture long-range dependencies between cluster identity for a current data point and the identities assigned to its neighbors.

At each time step t, the LSTM module takes in a data point x and a score vector a_{t-1} from previous time step t — 1 and outputs a new score a_t for the current time step. The score vector encodes the quality of the predicted label assigned to the data point x.
The network includes 4 LSTMs layers stacked on top of each other. The first three layers all have 64 units with residual connections, while the last layer can have the number of hidden units as either the number of clusters or the max number of possible clusters.

Meta-Clustering optimizes for a loss function that combines classification loss (L_classify) and local loss (L_local):

Φ refers to the architecture’s parameters, and λ refers to a hyper-parameter that controls the trade-off between the two losses.

The Meta-Clustering training algorithm in “Meta-Learning to Cluster.”

During each iteration in training, Meta-Clustering samples a batch of training data from the given pool of training tasks and feeds them into the LSTM network sequentially. The LSTM cell states are kept across epochs, enabling the LSTM network to remember the previously seen data points.

The Meta-Clustering inference algorithm in “Meta-Learning to Cluster.”

During testing, the LSTM network takes into each test task as inputs and returns the clustering as outputs. The data points in each dataset are shuffle across iterations to prevent potential prediction errors introduced by specific sequence orders.

From experiments on various synthetic and real-world data, Meta-Clustering achieves better clustering results than by using prevalent pre-existing linear and non-linear benchmark cluster losses. Additionally, Meta-Clustering can transfer its clustering ability to unseen datasets when trained on labeled real datasets of different distributions. Finally, Meta-Clustering is capable of approximating the right number of clusters in simple tasks and reducing the need to pre-specify the number of clusters.

8 — Self-Critique and Adapt (2020)

Antoniou and Storkey (the same authors of AAL) came up with Self-Critique and Adapt (SCA for short) that frames the problem of learning a loss-function using the set-to-set few-shot learning framework.

SCA enables meta-learning-based few-shot systems to learn not only from the support-set input-output pairs but also from the target-set inputs, by learning a label-free loss function, parameterized as a neural network.
Doing so grants the models the ability to learn from the target-set input data points, by merely computing a loss, conditioned on base-model predictions of the target set.
The label-free loss can be used to compute gradients for the model, and the gradients can then be used to update the base-model at inference time, to improve generalization performance.
Furthermore, SCA is model-agnostic and can be applied on top of any end-to-end differentiable, gradient-based, meta-learning method that uses the inner-loop optimization process to acquire task-specific information.

A unique proposition of SCA is that it follows a transductive learning approach, which benefits from unsupervised information from the test example points and specification by knowing where we need to focus on model capability.

The Self-Critique and Adapt architecture presented in “Learning to Learn via Self-Critique.”

As displayed in the figure above:

SCA takes a base-model, updates it for the support-set with an existing gradient-based meta-learning method, and then infers predictions for the target-set.
Once the predictions have been inferred, they are concatenated along with other based-model related information and are then passed to a learnable critic loss network. This critic network computes and returns a loss for the target-set.
The base-model is then updated with SGD for this critic loss.

This inner-loop optimization produces a predictive model specific to the support and target-set information. The quality of the inner loop learned predictive model is evaluated using ground truth labels from the training tasks. The outer loop then optimizes the initial parameters and the critic loss to maximize the quality of the inner loop predictions.

The Self-Critique and Adapt algorithm presented in “Learning to Learn via Self-Critique.”

The SCA algorithm is demonstrated to the left in the paper. The base model of choice is MAML++, which is parametrized as f(θ). The critic loss network is parameterized as C(W). The goal is to learn acceptable parameters θ and W such that f can achieve good generalization performance on the target set T after being optimized for the loss on the support set S.

From experiments on the miniImageNet and Caltech-UCSD Birds 200 datasets, the authors found that the critic network can improve well-established gradient-based meta-learning baselines. Some of the most useful conditional information for the critic model were the base model’s predictions, a relational task embedding, and a relational support-target-set network.

Conclusion

In this post, I have discussed the motivation for unsupervised meta-learning and the six papers that incorporate this learning paradigm into their meta-learning workflow. In particular, these papers can be classified into two camps:

CACTUs, UMTRA, AAL, and Unsupervised Meta-RL belong to the broad Unsupervised Meta-Learning camp. This camp aims to relax the conventional assumption of an annotated set of source tasks for meta-training, while still producing a good downstream performance of supervised few-shot learning. Typically, these synthetic source tasks are constructed without supervision via clustering (CACTUs) or class-preserving data augmentation (UMTRA and AAL).
Unsupervised Update Rules, Meta-Semi-Supervised Learning, Meta-Clustering, and SCA belong to the Meta-Learning Unsupervised Learning camp. This camp aims to use meta-learning to train unsupervised learning algorithms (Unsupervised Update Rules and Meta-Clustering) or loss functions (SCA) that work well for downstream supervised learning tasks. This helps deal with the ill-defined-ness of the unsupervised learning problem by transforming it into a problem with a clear meta supervised objective.

Stay tuned for part 4 of this series, where I’ll cover Active Learning!