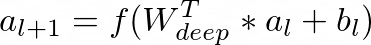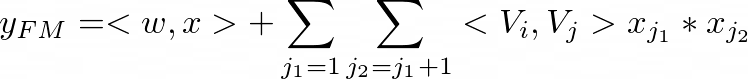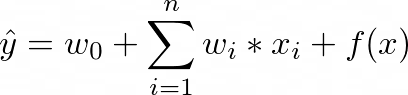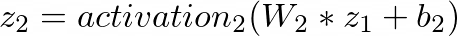Collaborative Filtering algorithms are most commonly used in the applications of Recommendation Systems. Due to the use of the Internet and the enormous amount of information that is generated, it becomes a very tedious task for users to find their preferences. Users’ preferences for items are represented in the form of a rating matrix, which is used to build the relation between users and items to find users’ relevant items. Thus, collaborative filtering algorithms nowadays face the problem with large datasets and sparseness in the rating matrix.

Among the various collaborative filtering techniques, matrix factorization is the most popular one, which projects users and items into a shared latent space, using a vector of latent features to represent a user or an item. After that, a user’s interaction on an item is modeled as the inner product of their latent vectors.

Despite the effectiveness of matrix factorization for collaborative filtering, it is well-known that its performance can be hindered by the simple choice of the interaction function: the inner product. For example, for the task of rating prediction on explicit feedback, it is well known that the performance of the matrix factorization model can be improved by incorporating user and item bias terms into the interaction function. While it seems to be just a trivial tweak for the inner product operator, it points to the positive effect of designing a better, dedicated interaction function for modeling the latent feature interactions between users and items. The inner product, which simply combines the multiplication of latent features linearly, may not be sufficient to capture the complex structure of user interaction data.

In this post and those to follow, I will be walking through the creation and training of recommendation systems, as I am currently working on this topic for my Master Thesis.

• Part 1 provided a high-level overview of recommendation systems, how they are built, and how they can be used to improve businesses across industries.

• Part 2 provided a careful review of the ongoing research initiatives concerning the strengths and application scenarios of these models.

• Part 3 provided a couple of research directions that might be relevant to the recommendation system scholar community.

• Part 4 provided the nitty-gritty mathematical details of 7 variants of matrix factorization that can be constructed: ranging from the use of clever side features to the application of Bayesian methods.

In Part 5, I explore the use of Multilayer Perceptron for collaborative filtering. A multi-layer perceptron is a feed-forward neural network with multiple hidden layers between the input layer and the output layer. It can be interpreted as a stacked layer of non-linear transformations to learn hierarchical feature representations. It is a concise but practical network that can approximate any measurable function to any desired degree of accuracy (a phenomenon known as Universal Approximation Theorem). As such, it is the basis of numerous advanced approaches and is widely used in many areas.

More specifically, I will walk through 5 papers that incorporate Multi-layer Perceptron into their recommendation framework.

1 — Wide and Deep Learning

Memorization and generalization are both critical for recommender systems. The paper “Wide and Deep Learning for Recommender Systems” (2016) by Google proposes a framework to combine the strengths of wide linear models and deep neural networks to address both issues. This framework has been production-ized and evaluated on the recommender system of Google Play, a massive-scale commercial app store.

As shown in the figure below, the wide learning component is a single-layer perceptron which can effectively memorize sparse feature interactions using cross-product feature transformations. The deep learning component is a multi-layer perceptron that can generalize to previously unseen feature interactions through low-dimensional embeddings.

Mathematically speaking, wide learning is defined as:

where y is the prediction, x is a vector of features, W is a vector of model parameters, and b is the bias. The feature set includes both raw inputs and transformed inputs (via cross-product transformation to capture the correlation between features).

In the deep learning component, each hidden layer performs the following computation:

where l is the layer number, f is the activation function, a_l is the vector of activations, b_l is the vector of biases, and W_l is the vector of model weights at the l-th layer.

The wide and deep learning model is attained by fusing these models:

where Y is the binary class label, W_{wide} is the vector of all wide model weights, W_{deep} is the vector of weights applied on the final activation a_{last}, and b is the bias term.

Full PyTorch implementation of this approach can be view here: https://github.com/khanhnamle1994/transfer-rec/tree/master/Multilayer-Perceptron-Experiments/Wide-and-Deep-PyTorch.

2 — Deep Factorization Machine

As an extension of the Wide and Deep Learning approach, “DeepFM: A Factorization-Machine Based Neural Network for CTR Prediction” (2017) by Huifeng Guo et al. is an end-to-end model that seamlessly integrates Factorization Machine (the wide component) and Multi-Layer Perceptron (the deep component). Compared to the Wide and Deep Model, DeepFM does not require tedious feature engineering.

As shown in the figure below, the Factorization Machine utilizes addition and inner product operations to capture the linear and pairwise interactions between features. The Multi-Layer Perceptron leverages the non-linear activations and deep structure to model the high-order interactions.

Mathematically speaking, the input of DeepFM is an m-fields data consisting of pairs (u, i) — which are the identity and features of user and item, as well as a binary label y that indicates user click behaviors (y = 1 means the user clicked the item, and y = 0 otherwise). The task here is to build a prediction model to estimate the probability of a user clicking a specific app in a given context.

For any particular feature i, a scalar w_i is used to weigh its 1st-order importance, and a latent vector V_i is used to measure its impact of interactions with other features. V_i is fed in the wide component to model 2nd-order feature interactions, and fed in the deep component to model high-order feature interactions. All parameters, including w_i, V_i, and the network parameters are trained jointly for the combined prediction model:

where y_hat is the predicted CTR (between 0 and 1), y_{FM} is the output of the wide Factorization Machine component, and y_{DNN} is the output of the Multi-Layer Perceptron component.

In the wide component, besides a linear (1st-order) interactions among features, the Factorization Machine models pairwise (2nd-order) feature interactions as the inner product of respective feature latent vectors. This helps capture 2nd-order feature interactions very effectively when the dataset is sparse. The output of Factorization Machine is the summation of an Addition unit and several Inner Product units:

with given features i and j. The Addition unit (first term) reflects the importance of 1st-order features, and the Inner Product units (second term) represent the impact of 2nd-order feature interactions.

In the deep component, the output of the Multi-Layer Perceptron looks like this:

where |H| is the number of hidden layers, a is the vector output of the embedding layer, W is the vector of model weights, and b is the vector of bias units.

Full PyTorch implementation of this approach can be view here: https://github.com/khanhnamle1994/transfer-rec/tree/master/Multilayer-Perceptron-Experiments/DeepFM-PyTorch.

3 — Extreme Deep Factorization Machine

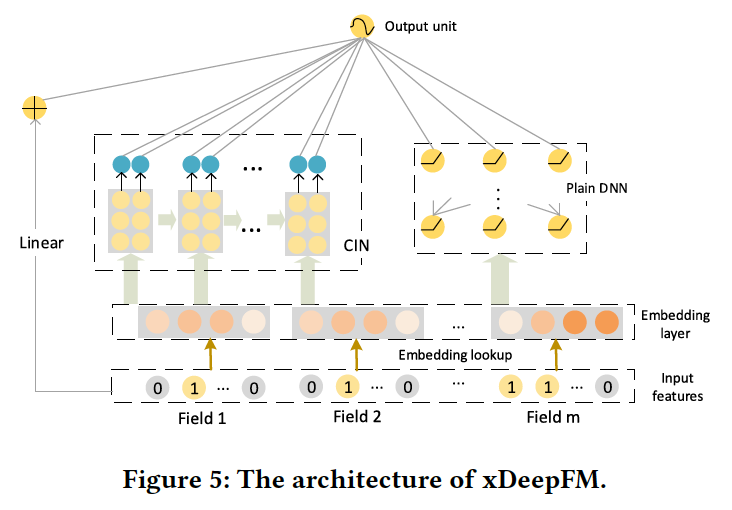
As an extension of the Deep Factorization Machine, “xDeepFM: Combining Explicit and Implicit Feature Interactions for Recommender Systems” (2018) from Jianxun Lian et al. can jointly model the explicit and implicit feature interactions. The explicit high-order feature interactions are learned via a Compressed Interaction Network, while the implicit high-order feature infractions are learned via a Multi-Layer Perceptron. This model also requires no manual feature engineering and releases data scientists from tedious feature searching work.

The Compressed Interaction Network is designed with the following considerations:

1. Interactions are applied at a vector-wise level, not at the bit-wise level.

2. High-order feature interactions are measured explicitly.

3. The complexity of the network will not grow exponentially with the degree of interactions.

The structure of the Compressed Interaction Network is very similar to the Recurrent Neural Network, where the outputs of the next hidden layer are dependent on the last hidden layer and additional input. The structure of embedding vectors at all layers is kept in the status quo; thus, the interactions are applied at the vector-wise level.

• Looking at the figure 4a above, the intermediate tensor Z^{k+1} is the outer products along each embedding dimension of the hidden layer x^k and original feature matrix x⁰. The process to calculate each hidden layer x^k has a strong connection with the well-known Convolutional Neural Network in computer vision. Here, Z^{k+1} can be regarded as a special type of image, and W^{k, h} is a filter.

• As seen in figure 4b, the authors slide the filter across Z^{k+1} along the embedding dimension and get a hidden vector x^{k+1} — which is usually called a feature map in computer vision. Therefore, x^k is a collection of H_k different feature maps.

• Figure 4c provides an overview of the architecture of the Compressed Interaction Network. Let T denote the depth of the network. Every hidden layer X^k has a connection with output units. The authors apply sum pooling on each feature map of the hidden layer and get a pooling vector p^k with length H_k for the k-th hidden layer. All pooling vectors from hidden layers are concatenated before connected to output units: p+ = [p¹, p², …, p^T]

xDeepFM combines the Compressed Interaction Network above with plain Multi-Layer Perceptrons via the wide and deep learning framework. On the one hand, this model includes both low-order and high-order feature interactions; on the other hand, it also contains both implicit and explicit feature interactions. The architecture is shown here.

Mathematically speaking, the resulting output unit is:

where a is the vector of raw features, x_{mlp} is the vector of outputs from the plain Multi-Layer Perceptron, p+ is the vector of outputs from the Cross Interaction Network. W and b are the learnable parameters — weights and biases, respectively.

Full PyTorch implementation of this approach can be view here: https://github.com/khanhnamle1994/transfer-rec/tree/master/Multilayer-Perceptron-Experiments/xDeepFM-PyTorch

4 — Neural Factorization Machines

Another parallel work that seamlessly integrates Factorization Machines and Multi-Layer Perceptron is Xiangnan He and Tat-Seng Chua’s “Neural Factorization Machines for Sparse Predictive Analytics” (2017). This model brings together the effectiveness of linear factorization machines with the strong representation ability of non-linear neural networks for sparse predictive analytics.

As seen below, the key to its architecture is an operation called Bilinear-Interaction pooling that allows a neural network model to learn more informative feature interactions at the lower level. Through stacking non-linear layers above the Bilinear-Interaction layer, the authors were able to deepen the shallow linear Factorization Machine, modeling higher-order, and non-linear feature interactions effectively to improve Factorization Machine’s expressiveness. In contrast to traditional deep learning methods that simply concatenate or average embedding vectors in the low level, this use of Bilinear-Interaction pooling encodes more informative feature interactions, greatly facilitating the following “deep” layers to learn meaningful information.

Let’s dive into the math of the Neural Factorization Machine model. Given a sparse vector x as input, the model estimates the target as:

where the first term models global bias of data of features, the second term models global bias of weight of features, and the third term f(x) is a Multi-Layer Perceptron (as shown in figure 2) that models feature interactions. The design of f(x) consists of these layer components:

Embedding Layer

This is a fully-connected layer that projects each feature to a dense vector representation. Let v_i be the embedding vector for the i-th feature. Then after the embedding step, the authors obtain a set of embedding vectors to represent the input feature vector x.

Due to the possible sparse representation of x, the authors only include the embedding vectors for non-zero features, where x_i does not equal to 0.

Bilinear-Interaction Layer

Then the embedding set V_x is fed into a Bilinear-Interaction layer, which is a pooling operation that converts a set of embedding vectors to one vector:

where v_i.x_j denotes the element-wise product of two vectors v_i and x_j. The output of this pooling is a k-dimension vector that encodes the second-order interactions between features in the embedding space.

Hidden Layers

Above the Bilinear-Interaction pooling layer is a stack of fully-connected layers, which are capable of learning higher-order interactions between features. The definition of these hidden layers is:

where L is the number of hidden layers; W_L, b_L, and activation_L correspond to the weight matrix, bias vector, and activation function for the l-th layer, respectively. The choice of activation functions can be sigmoid, tanh, or ReLU to learn higher-order feature interactions non-linearly.

Prediction Layer

Lastly, the output vector of the last hidden layer z_L is transformed into the final prediction score:

where h^T denotes the neuron weights of the prediction layer.

Full PyTorch implementation of this approach can be view here: https://github.com/khanhnamle1994/transfer-rec/tree/master/Multilayer-Perceptron-Experiments/Neural-FM-PyTorch

5 — Neural Collaborative Filtering

The paper “Neural Collaborative Filtering“ (2018) by Xiangnan He et al. pushed the use of multi-layer perceptrons for learning the interaction function from data one step further. Note here that they are also the same authors of the Neural Factorization Machine paper mentioned above. They formalized a modeling approach for collaborative filtering that focuses on the implicit feedback, which indirectly reflects users’ preference through behaviors like watching videos, purchasing products, and clicking items. Compared to explicit feedback such as ratings and reviews, implicit feedback can be tracked automatically and is thus much more natural to collect for content providers. However, it is more challenging to utilize since user satisfaction is not observed, and there is an inherent scarcity of negative feedback.

The user-item interaction value y_ui to model users’ implicit feedback can be either 1 or 0. A value of 1 indicates that there is an interaction between user u and item i, but it does not mean u likes i. This poses challenges in learning from implicit data since it provides only noisy signals about users’ preferences. While observed entries at least reflect users’ interest in items, the unobserved entries can be just missing data, and there is a natural scarcity of negative feedback.

The authors adopt a multi-layer representation to model a user-item interaction y_ui, as shown below, where the output of one layer serves as the input of the next one.

• The bottom input layer consists of 2 feature vectors that describe user u and item i, which can be customized to support a wide range of modeling of users and items. In particular, the paper uses only the identity of a user and an item as the input feature, transforming it into a binarized sparse vector with one-hot encoding. With such a generic feature representation for inputs, this framework can be easily adjusted to address the cold-start problem by using content features to represent users and items.

• Above the input layer is the embedding layer — a fully connected layer that projects the sparse representation to a dense vector. The obtained user/item embedding can be seen as the latent vector for user/item in the context of the latent factor model.

• The user embedding and item embedding are then fed into a multi-layer neural architecture (termed Neural Collaborative Filtering layers) to map the latent vectors to prediction scores. Each layer of the neural collaborative filtering layers can be customized to discover the specific latent structure of user-item interactions. The dimension of the last hidden layer X determines the model’s capability.

• The final output layer is the predicted score y-hat_ui, and training is performed by minimizing the pointwise loss between y-hat_ui and its target value y_ui.

The above framework can be summed up with the scoring function below:

where y-hat_ui is the predicted score of interaction y_ui, and theta denotes the model parameters. f is the multi-layer perceptron that maps model parameters to the predicted score. More specifically, P is the latent-factor matrix for users, Q is the latent-factor matrix for items, v_u^U is the side information associated with user features, and v_i^I is the side information associated with item features.

The paper argues that traditional matrix factorization can be viewed as a special case of Neural Collaborative Filtering. Therefore, it is convenient to fuse the neural interpretation of matrix factorization with Multi-Layer Perceptron to formulate a more general model which makes use of both linearity of Matrix Factorization and non-linearity of Multi-Layer Perceptron to enhance recommendation quality.

Full PyTorch implementation of this approach can be view here: https://github.com/khanhnamle1994/transfer-rec/tree/master/Multilayer-Perceptron-Experiments/Neural-CF-PyTorch-Version2.

Model Evaluation

You can check out all five multi-layer perceptron-based recommendation models that I built at this repository: https://github.com/khanhnamle1994/transfer-rec/tree/master/Multilayer-Perceptron-Experiments.

• The dataset is MovieLens 1M, similar to my Matrix Factorization experiments in my last article. The goal is to predict ratings of a user for a particular movie — where ratings are on the 1 to 5 scale.

• The only difference is that, to use the Factorization Machine-based models that are designed for click-through rate prediction, I use binary ratings. Ratings less than equal to 3 are deemed to be 0, and ratings bigger than 3 are considered to be 1.

• The evaluation metric, therefore, is AUC, considering this is a binary classification problem (instead of RMSE like last time).

• All models were trained for 100 epochs, and the results were captured in Weights and Biases. For those that are not familiar, it is a brilliant tool that stores all model hyper-parameters and output metrics in one place to track experiments and reproduce results effortlessly.

The result table is at the bottom of the README, and as you can see from the Weights and Biases dashboard visualization:

• Wide and Deep Learning model has the best AUC result in both test and validation set.

• On the other hand, extreme Deep Factorization Machine has the lowest AUC, respectively.

• Neural Collaborative Filtering has the fastest runtime, and extreme Deep Factorization Machine has the slowest runtime.

Conclusion

In this post, I have discussed the intuitive meaning of Multi-Layer Perceptron and its use in collaborative filtering. I also walked through 5 different papers that use MLP for the recommendation framework: (1) Wide and Deep Learning, (2) Deep Factorization Machine, (3) Extreme Deep Factorization Machine, (4) Neural Factorization Machine, and (5) Neural Collaborative Filtering. These models complement the mainstream shallow models for collaborative filtering, thus opening up a new avenue of research possibilities for recommendations based on deep learning.

Stay tuned for future blog posts of this series that go beyond discriminative models and enter the realm of generative models for collaborative filtering.

References

• Wide and Deep Learning for Recommender Systems. Heng-Tze Cheng, Levent Koc, Jeremiah Harmsen, Tal Shaked, Tushar Chandra, Hrishi Aradhye, Glen Anderson, Greg Corrado, Wei Chai, Mustafa Ispir, Rohan Anil, Zakaria Haque, Lichan Hong, Vihan Jain, Xiaobing Liu, and Hemal Shah. June 2016

• DeepFM: A Factorization-Machine based Neural Network for CTR Prediction. Huifeng Guo, Ruiming Tang, Yunming Ye, Zhenguo Li, and Xiuqiang He. March 2017.

• Neural Collaborative Filtering. Xiangnan He, Lizi Liao, Hanwang Zhang, Liqiang Nie, Xia Hu, and Tat-Seng Chua. August 2017

• Neural Factorization Machines for Sparse Predictive Analytics. Xiangnan He and Tat-Seng Chua. August 2017

• xDeepFM: Combining Explicit and Implicit Feature Interactions for Recommender Systems. Jianxun Lian, Xiaohuan Zhou, Fuzheng Zhang, Zhongxia Chen, Xing Xie, and Guangzhong Sun. May 2018